How to calculate your odds in poker
In today's article, we'll cover a very basic, still crucial concept: knowing your odds. Understanding this will help you make better decisions at the table and give you some fundamental knowledge about when to call, for example.

What are pot odds?
The term' pot odds' refers to the ratio between the size of the pot and the size of the bet you need to call.
Let's say you play NL100 cash game and are facing a river bet. The pot contains $20, and Villain bets $10 into it. So then, you need to call $10 to win $30, which is 30:10 or simplified 3 to 1.
Another way to put this; after we make the call, the total pot will be $40. Then we need to divide the $10 call we have to make with the total size of the pot ($40), which gives us 0.25. If we multiply this by 100, we'll get the actual pot odds of 25%.
In a hand like this, you'll need at least 25% of equity to make a profitable call.
How to use pot odds?
There are numerous spots when calculating pot odds that will help you to make the correct decision.
For example, you can calculate certain preflop decisions based on the abovementioned formula. There are two caveats for this. One of them is that it's not practical in-game, and the second is its limitations. You need to know the exact ranges and to close the action.
So in a preflop example, against a specific open size, you can calculate your pot odds with a certain hand if it will be profitable to call. But you cannot estimate other players' actions, so it will work only from the BB as closing the action. Besides that, you will get an answer as the call if it is mathematically profitable or not. Still, other factors might make that specific hand a better candidate to 3-bet or even to fold due to poor EQ realization. (We'll discuss this in the following article)
Other situations where pot odds calculation comes in handy also require that the action is closed by you. These could be spots when you have a draw or a river decision when you need to estimate if you have the correct odds to call.

Let's say you have 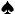 A
A 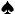 K on a
K on a 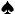 Q
Q 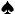 J
J  2 board. You'll make the nuts on every spade (9 outs) and every T (3 outs). Check out the article on calculating outs, in case you missed it. We'll not consider now that hitting a top pair or ace high might be enough at showdown. So you have 12 outs, and your opponent bets on the flop $15 into a $21 pot.
2 board. You'll make the nuts on every spade (9 outs) and every T (3 outs). Check out the article on calculating outs, in case you missed it. We'll not consider now that hitting a top pair or ace high might be enough at showdown. So you have 12 outs, and your opponent bets on the flop $15 into a $21 pot.
The math from above gives you the following:
pot + bet + your call = final pot
$21 + $15 + $15 = $51
call / final pot = EQ*100
$15 / $51 = 29,4%
So, in this case, you’ll need roughly 29% EQ to continue. If we use our simplified odd calculation;
EQ = (number of outs x 4) – (number of outs – 8)
we can see that 12 outs give us around 44%. And these are only the cases when we hit the stone-cold nuts. This means our EQ is way higher than the pot odds given; our call will be profitable.
However, stack and bet sizes can vary, the ratio of a specific bet size and the EQ required to make a profitable call will remain the same. So you can even memorize the most common numbers to save time at the table;
|
Bet size compared to the pot |
EQ required |
|
25% |
16% |
|
33% |
20% |
|
50% |
25% |
|
66% |
28% |
|
100% |
33% |
|
150% |
37,5% |
|
200% |
40% |
For instance, you face a river bet the size of the pot. You will need 33% EQ to make a profitable call. In a situation when your opponent is perfectly polarized (he either has a nutted hand or an air hand) and you have a pure bluff catcher (beating all the bluffs and none of the value bets), he will need to bluff at least 33% of the time to make your bluff catcher profitable to call.
Summary
Pot odds are an essential notion in poker terminology. You need to know your odds to make a correct decision. Sometimes, it’s very straightforward to calculate, especially when we are closing the action. However, we saw limitations and other factors that could influence what is, quote on quote, the highest EV decision. That’s why we’ll continue exploring the topic in the following article by introducing terms such as implied- and reversed implied odds, EQ realization, etc.
Hopefully, you found this article useful!
Good luck at the tables!















0 comments