Begginer Guide: What is implied odds, reversed implied odds in poker?
In the previous article, we discussed a phenomenon called pot odds. Although it is crucial to understand the concept of pot odds (PO), it has a huge problem. Its use is very limited to situations where the action is closed by the last bet, while in poker, this spot is less frequent (mostly river decisions and all-in situations) than others. Today, we’ll introduce the concept of implied odds (IO) to find a mathematical solution for the rest of the spots.

What are implied odds?
Implied odds are bets/money you expect to win on future streets. It's pretty complicated and involves a lot of guessing. Still, you can define the exact amount needed for a call or a bet. The most common situation is when you have a draw but don't have the correct pot odds to make a profitable call.
Let's say you play NL100 and have 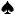 T
T 9 on ,
9 on ,  A
A 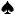 8
8  7
7 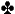 2 and your opponent bets $10 into a $15 pot. If you remember how to calculate pot odds, you might come up with the formula:
2 and your opponent bets $10 into a $15 pot. If you remember how to calculate pot odds, you might come up with the formula:
10 / (10 + 15 + 10) x 100 = ~28,6%
Thus, you need at least 28,6% of EQ to make a good call. However, you have 8 "clean" out to the nuts, which only gives you around 16%.
In order to calculate with implied odds, we need to introduce another equation fairly similar to the one for pot odds:
Implied Odds: Call / (Bet + Pot + Call + Y) = EQ
Basically, it's the same calculation; we only introduce the "unknown Y". By solving the equation,' Y' will give us the amount we need to win on later streets (in this case, on the river) to justify our turn call.
Let's solve it for our example!
10 / (10 + 15 +10 + Y) = 0,16
10 / (35 + Y) = 0,16
0,16 x 35 + 0,16Y = 10
0,16Y = 4,4
Y = 27,5
So, we need to win $27,5 extra on the river to make our turn call profitable. Note that we don't calculate here when we hit a pair, and it's enough to win the hand, neither with the possibility that we bluff out our opponent on the river. This amount refers to when we hit our flush (aka nuts) and win at the showdown.
Here, you'll need to estimate how likely this outcome is realistic. By the river, the pot will be $35, and you'll need to win $27,5 (roughly 3/4 pot) more on average. All possible variations make this a reasonable bet size on the river:
- Villain could be bluffing, in which case he should use a similar sizing.
- Again, he could be value-betting a worse hand (such as sets, top 2 pairs, etc.) for a reasonable size.
- He could decide to check-call with hands that are too thin for value-betting but still reasonable bluff catchers, such as AQ, A9, etc.
In our example, calculating with implied odds seems like a justifiable turn call with our open-ended straight draw.
Of course, you can calculate with implied odds in other situations, not just defending with draws. Even as the preflop raiser, you can estimate implied odds and compare the EV and probability of various lines. We saw limitations in calculating implied odds; we still have yet to discuss another aspect.

What are reversed implied odds?
Sometimes, even though you count with only clean outs, you’ll be outdrawn or make the second-best hand. The two primary examples are when you hit a flush or straight with low cards, and your opponent shows up with a stronger flush or a higher straight. The other is a spot when you hit your straight or flush with your draw, when your opponent holds two pairs or a set, while one of your outs gives them a full house or quads. Moreover, if you hit your hand on the turn, there is still a fair chance for your opponent to redraw to full houses.
All these situations, when you calculate with implied odds but a fraction of it actually works for your opponent, are called reversed implied odds.
Why it’s more complicated than that?
As we mentioned in some instances, we simplified the examples. The theoretically optimal play is a lot more complicated because it considers all the factors we omitted here. For example, it’s challenging to nominalize:
- How often your opponent gives up a bluff.
- Your high hand is enough at the showdown without improving.
- Your opponent deviates from the optimal play, etc.
Some hands realize EQ better, especially in position. So there will be a considerable difference in calculating implied odds depending on positions. Just think about this: you hit your flush by the river but are out of position. When a possible flush is out there, will your opponent put another bet (the necessary amount, the one you counted as IO)? Or you start to develop a donk betting range? Are they going to pay that off?
Summary
Those who understand (and apply correctly!) the implied odds phenomenon will have a significant advantage. IO is an essential part of the game, use it correctly, and you'll win extra bets. However, if you use it to justify loose, theoretically horrible plays, you'll experience some big losses. You have the formula;
Call / (Bet + Pot + Call + Y) = EQ,
so you'll get a precise, indisputable number of how much more you need to win. It's crucial how well you assess the situation and whether it's a profitable outcome.
We highly suggest reading this article again and testing your calculations on real examples, away from the tables!
Good luck applying implied odds in your game!















0 comments